双边装配线里面一个基本的问题就是找到最佳节拍,解决了这个问题相当于解决了大部分的问题,因为求解思路基本是比较相近的。本篇我们讨论加入了一些约束,有一定的复杂性,要求算法可以很好的兼容约束。基本上目前的算法都是属于贪婪(Iterated Greedy)算法,为了收缩广大的搜索域。
Introduction
A pair of face-to-face stations like station (n,1) and station (n,2) is called a mated-station and one of them is the companion of the other. The idle time on each station can be divided into two types: Sequence-dependent idle time and the remaining idle time existing at the rear of the last task. There are other assignment restrictions which exist in real applications need to be considered, including zoning restriction, synchronous restriction, positional restriction, distance restriction and resource restriction. We focus on zoning restriction, synchronous restriction, positional restriction which are usually found in real applications.
Zoning restriction: consist of positive zoning restriction and negative zoning restriction. Positive zoning restriction means that some tasks need to be assigned to the same station while negative zoning restriction prohibits (禁止) some tasks being allocated to the same mated-station.
Synchronous restriction: restrict two operators to perform a pair of tasks simultaneously on both sides of the same mated-station for collaboration. (facing directly and have the same starting time)
Positional restriction: indicates that certain tasks need to be allocated on predetermined stations or mated-stations.
Mathematical Model
Assumptions
- A single model is taken into account and the travel time between stations is ignored.
- Precedence diagrams are known and deterministic
- The task with a positional restriction should be assigned to the predefined station.
- The tasks in the positive zoning restriction should be assigned to the same station.
- The tasks in the negative zoning restrictions are prohibited to be allocated to the same mated-station
Mathematical form
The objective function is as follow:
$nm$ 表示number of mated-stations. J表示所有配对位置,K表示所有方位(左工位和右工位),$SF_{jk}$ and $ST_{jk}$ 分别表示该工位的最后一个任务的完工时间和所有任务的作业时间和。上面的目标函数分为四个部分:第一部分表示最小化剩余空闲时间,第二部分表示最小化序列空闲时间,第三部分和第四部分表示各个位置之间的上述两个空闲时间的平衡(平方项求和中最大项和最小项的比值显示了平衡程度)。
Encoding and Decoding
采用位置编码无疑是双边装配线固定位置数目一个比较好的方法,被广泛的应用,最终还是要确定任务的分配顺序和方位。我们提出一种优先权编码机制,在解码的过程中我们采用基于优先权链的启发式规则。我们通过调整任务的优先权重来减少序列空闲时间。当然我们还需要考虑任务的约束,这是我们一个创新点。
Initial Priority Value Adjustment(Encoding)
所有任务优先权都在区间[0,1]。比如著名的RPW 启发式算法权重定义:任务和所有后续的作业时间和。我们首先将所有任务按照一定权重降序排列,然后任务$i$ 的先验概率$PL[i]$ 可以通过下式计算:
其中$TS_i$ 表示任务i在排序中的序号,$nt$ 表示任务的数目。这样权重越大的任务先验概率越大。当然我们也可以在搜索的过程中改变任务的权重(这就是本文编码的实质),然后根据新的权重更新先验概率。
Task Assignment Rule
任务的分配规则是用来降低序列空闲时间和平衡负荷的。首先,我们寻找不会增加序列空闲时间的任务,提高这些任务的权重(减小会产生序列空闲时间的任务权重);同样如果一个任务分配可以使得该工位的结束时间(就是这个任务的结束时间)位于区间[Cm,CT]时,我们也提高这个任务的权重。其中Cm表示位置的平均负荷,计算方法如下:$Cm=\sum_{i\in I}t_i/2nm$ . 这样负荷会比较平衡,因为所有位置的负荷都在这个区间内波动。
这个算法的顺序如下:
计算先验概率
$PL[i] =PL[i]+1$ if task i satisfies cycle time,direction,and precedence restrictions while $j\neq nm$ or satisfies only direction and precedence restrictions while $j=nm$
(仅仅是要满足节拍、方位、先序约束)
if PL[i]>1 and task i in the assignable task set can begin at the earliest start time of the current station, then $PL[i] =PL[i]+1$ (需要现在就可以分配的任务,就是不会产生序列空闲时间的任务优先,如果现在左右结束时间一样,那么所有没有先序的任务权重都加1,最后一个位置不考虑节拍约束是为了让所有任务都分配,结果一定是可行的)
if PL[i]>1 and the finishing time of task i in the assignable task set is in [Cm,CT], then $PL[i] =PL[i]+1$
经过以上步骤后有三种情况:$PL[i]<1$表示任务i不能分配;$1<PL[i]<2$ 表明任务i可以分配但是权重没有被提升;$PL[i]>2$ 表明任务可以分配并且优先分配
Positional Restriction Handling
首先我们来看一下固定任务约束,if the current station is the predetermined station $(j^\ast,k^\ast)$ ,the priority of the task is increased. 为了实现这个目标,我们构建了一个矩阵TS,定义如下:
那么任务i的概率更改为:$PL[i]=PL[i]+TS[i][j][k]$ 这样如果在固定位置之前的配对位置,任务i的概率$PL[i]<1$ 所以任务不会被分配。如果当前位置正好是预先设定的位置,任务i的概率会被增加。 当然,也可能存在任务i并不能分配到预先定义的位置的情况,所以我们对于后面的位置不加约束,为了就是能够得到一个可行解,这种定义方便了编程操作难度。
Positive Zoning Restriction Handling
前面有人将这样的任务看做一个整体分配,虽然降低了难度,但是这样顺序一定会带来结果上的差距,所以我们不考虑这样的方法。符合前面的规范性,我们同样定义一个矩阵TT来实现这个约束:
for task i, if PL[i]>1(首先要确认可以分配), its priority is updated as follow:
其中NT表示station(j,k)已经分配的任务数目,$T_h$ 表示当前工作站分配的第h个任务。这个调整表明如果当前位置至少存在一个PZ任务,那么这个任务的权重就会上升,当然我们也无法保证PZ任务对一定能完全符合约束,只能在最大限度上保证。
Decoding Scheme(Priority based)
- Set the initial cycle time $CT_{initial}$
- Open a new mated-station
- Choose a side with greater capacity(default select left side)
- Update the priority values with task assignment rule
- If task i, $i\in I$ is not in the negative zoning restriction, go to next step. Else if PL[i]>1 and other task has been allocated to the current mated-station, then $PL[i]=Pl[i]-\psi$ (其实吧这里可以同PZ一样操作,从数学上更加简洁一点)
- If PL[i]>1, then $PL[i]=PL[i]+TS[i][j][k]$
- If PL[i]>1, then $PL[i]=PL[i]+\sum_{h=1}^{NT}TT[i][T_h]$ (这里和上一步分开操作,因为上一步如果不可行这一步就没有必要了,其实固定任务和PZ任务不会出现在一起,所以一起操作也无妨)
- If task i, $i\in I$ is not in the synchronous restriction, go to next step. Else, if task i,h in synchronous restriction can be assigned, then assign the two tasks and go to step 10; otherwise, $PL[i]=Pl[i]-\psi$ (很简单了,如果两个任务都可以分配了,赶紧分配,否则降低概率,延后等待)
- 如果所有任务的概率都小于1,那么换边。重新执行步骤4-7. 如果同样没有可分配的任务,回到步骤2,而如果另外这边有可以分配的任务,选择权重最大的任务放入。
- 如果任务分配还没结束,回到步骤3。否则选择最晚的结束时间作为当前的节拍,更新初始的节拍(个人备注:更新的规则很多,可以是相加取平均值等)
初始的节拍生成方式为:$CT_{initial}=\alpha\times Cm (\alpha>1)$ 本文选择的更新节拍规则为$CT_{initial}=CT_{current}-1$ 这样我们就可以逐步获得最佳的节拍。
Cost refine
在解码的过程中,the synchronism restriction and the negative zoning restriction are satisfied while positive zoning restriction and positional restrictions may be violated. 所以我们更新目标损失函数如下:
其中$np$ and $npz$ 分别是违反规则的任务数目,惩罚系数待定。为了让所有任务都满足约束,我们将惩罚系数设置一个很大的数,比如1000
Iterated Greedy Approach
编码(优先权编码)和解码的规则都定好了,就差一个搜索的框架了。我们使用的迭代贪婪搜索方法:首先从一个比较不错的初始解(准确的说是初始的优先权编码)开始,然后随机拆解任务(remove some tasks) 然后用一定的方法重构解(reconstruction: reinserts tasks back). 这样我们获得了一个新的解,然后我们利用一定的规则接受新解和保留旧解,可能我们还会用一定的规则搜索局部更优解。这样一套操作确定:拆解->重构->接受域->局部搜索。我们不断循环这个步骤直到停止,下面是更加详细的介绍。
Initialize by modified NEH Heuristic
其实这就是一个Sequence Minimize Optimization(按照的序列编码):
- generate an initial task permutation(排列) $\pi(\pi=[\pi_1,\pi_2,…,\pi_n])$ with RPW heuristic (通过权重选择,可以是随机轮流的权重)
- remove the 2nd task i from $\pi$ and obtain the solution by inserting it into position 1. Then the better one is selected.(比如可以用我们之前的目标函数)
- remove the remaining tasks i(i>2) and obtain the best solution by inserting it to all the positions before its incumbent(现在的位置).
Improved local search
以下过程基于优先权编码。我们选择一个任务k,把这个任务移出当前的位置,然后插入到所有可行的位置,如果有改进,那么以新的解代替旧的解。我们循环整个算法直到没有改进可以发生。

上面算法目的在于找到局部最优解,但是它可能会错过局部最优解,因为不一定所有的任务都能被遍历,而且这个算法很耗时,因为它需要遍历所有可以插入的位置。为了克服第一个缺点,我们按照一定顺序($\pi^{rp}$)选择所有的任务进行考察。实验证明最佳的序列顺序比随机序列顺序策略要好,所以我们选择最佳的序列作为参考策略。对于第二个缺点,核心在于减少无效解码 ,但是我们还是要保留搜索局部最优解的能力。所以我们在选择插入位置的时候应该选择满足所有先序和所有后续约束的位置(其实每次只改变一个任务,我们只需要满足紧邻先序和紧邻后续就可以了)。
深度解读:其实这里的第二条规则对于初始化的优先权编码有依赖性。我们完全可以生成不满足先序约束的优先权链(但是这是没有必要的),这样第二部分的改进就无从下手,相当于废弃。为什么说最好能够满足先序约束呢?因为当一开始就满足先序约束的时候,我们移动一个任务的权重到新位置k即使超出先序约束的范围[a,b],即$K\notin [a,b]$ ,由于分配的时候仍然要考虑先序约束,所以效果相当于$k=cut(k,a,b)$ ,所以我们每次选择更好的权重优先级位置的时候只要在满足约束的位置之间考虑就行了。下面说说这里的初始化优先权为什么是满足先序约束的。很简单,我们用的初始化权重是任务和其所有后续的作业时间和,显然这样得出的能够满足先序。这样在初始化权重编码的时候用到的局部优化方法也应该在满足先序约束的范围内考虑。

Destruction,Reconstruction and Acceptance Criterion
为了跳出局部最优解,我们需要拆解与重构得到新的解。
Destruction phase
前人的做法是随机选择d个任务从当前序列$\pi$ 中删除,加入到移除的序列$\pi_R$,我们这里稍作改变。我们将每次移除的任务加入到序列的末尾,这样保证了每一次的任务序列都能得到一个可行解。
Reconstruction phase
移到后面的任务一个个往前移动到最佳的位置。移动完成之后我们进行local search得到局部最优解
Acceptance Criterion
比现在好直接接受,比现在差我们以一定概率接受,其中有一个温度常数$T=T_0\sum_i^n t_i/100nm$
Note
注意到参数d(移除的任务数目)和参数T都是很重要的参数。一个大的d可能会导致一个完全全新的解,而一个小的d可能无法跳出局部最优解。同理,一个大的T可能会接受很差的解,一个小的T可能无法容忍一个新的解。

最后选择的参数 $(w_1,w_2,w_3,w_4)=(10,5,1,1)$ 终止的条件设为 $t=nt\times nt \times\rho \;ms$ 其中参数$\rho=15$
Result
有两个需要比较的点:其一就是 The priority-based decoding method,其二就是 the new methods to deal with assignment restrictions.
Coding
设计了两个参数一样的GA算法,其中GA1是传统的位置编码,GA2采用的是本文的优先权编码。我们提出了一个a nonparametric Wilcoxon matched-pairs signed rank test。所有的结果都通过以下方式进行转换:the best result assigned to rank 1 while the worst result in marked with rank 2. 结果经过多次重复计算后得到 the average rank for GA2 with the proposed decoding is 1, which proves the superiority of the proposed decoding scheme.
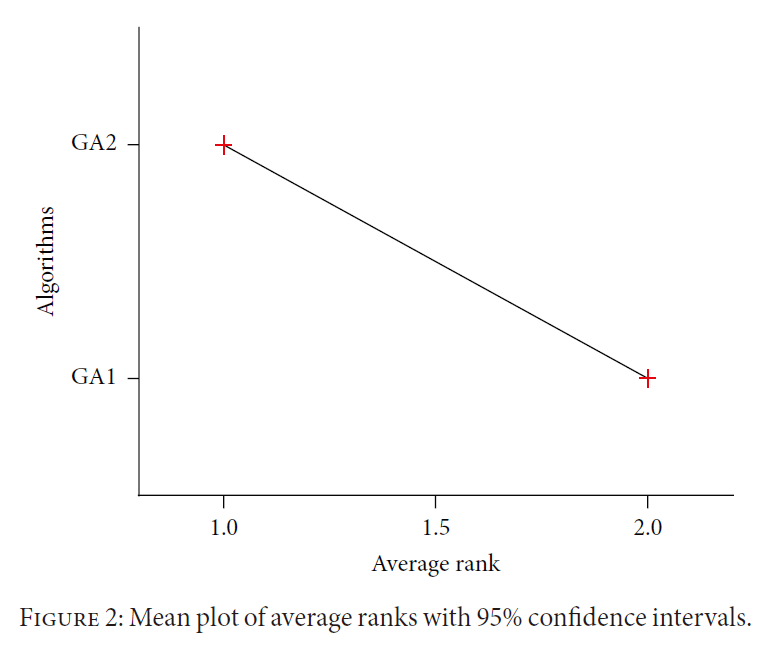
其实上,GA1算法总没法有效的减少序列空闲时间,因为它只是采用了一个简单的权重。相反,现在的解码方式考虑到了序列空闲时间和负荷的动平衡。
Restriction method
我们同样设计了两个GA算法,其中一个GA3采用别人发表的约束方式,GA4采用本文的约束方式。通过计算,GA4 outperforms the GA3 for all the cases. 主要有两个原因:新的约束算法提高了得到满足约束解的可能性;PZ的任务不是直接绑定在一起,减少了序列空闲时间。
Calibration(校准) of IG
我们参数d和T的选择有以下两个范围 $d\in (4,8,12,16);\;\; T0\in(0.1,0.5,1.0,5.0)$ 因为包含了不同的问题,所以我们每个问题都选择了最佳的参数。我们采用RDI来描述每个参数得到结果的好坏,完成了所有测试后,我们采用average RDI value of each case for statistical analysis. (每个的测试次数可选40次)
其中的计算都是指代fitness。比如205问题我们得到了如下的分布:
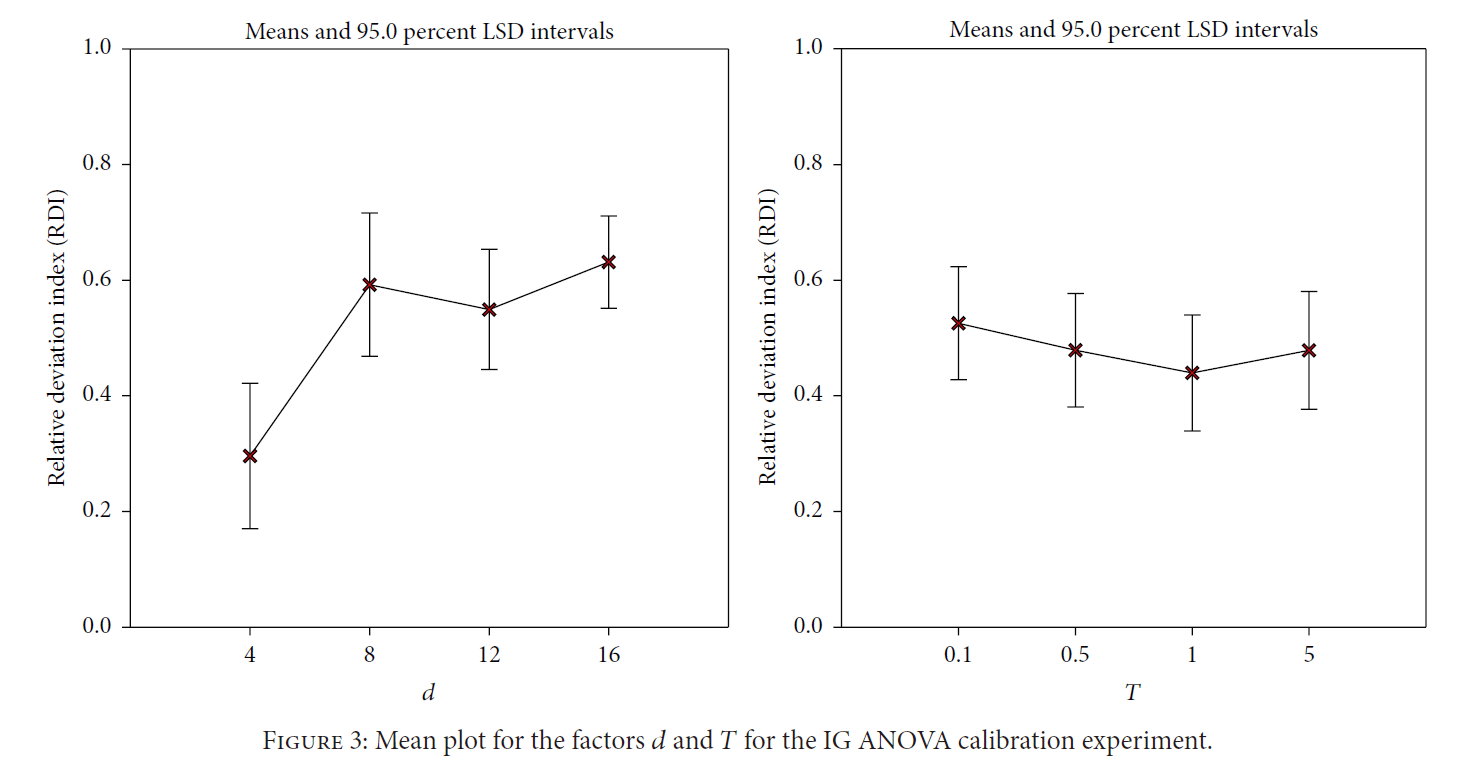
(把所有参数得到的结果放在一起,相同的位置数目)从图中我们可以得出选择d=4,在此基础上选择T=1。结果对比上不仅要考虑最佳性能,也要考虑平均性能或者方差。
Summary and Conclusion
In this paper, a simple and effective iterated greedy (IG) algorithm is developed for the two-sided assembly line balancing problem type-II (TALBP-II) with assignment restrictions. The NEH heuristic is modified for TALBP-II as the initialization procedure. A new local search with referred permutation is developed, and acceleration by eliminating the insert operator that conflicted with precedence restrictions is developed to speed up the search process while preserving the ability of finding a local optimum.
A new priority-based decoding scheme is also proposed to reduce sequence-dependence idle time, balance the workload, and deal with assignment restrictions. To be specific, the task assignment rules are embedded into the decoding scheme to reduce sequence-dependent idle time and balance the workload on each station. A new method to deal with the positional restriction increase the possibility of finding a feasible solution by preventing assigning the tasks with positional restriction to the former mated-station of the predetermined one. And a new method to deal with positive zoning restriction is applied to further reduce the sequence dependent idle time by allocating the tasks with positive zoning restriction separately.
The priority-based encoding and decoding, especially the methods to reduce idle times and deal with assignment restrictions,may be modified to address other two-sided assembly line problem.
总结恰到好处,指出了关键的Skill,并且指出可以利用的部分价值。
Reference
Deep inside
P1: 优先权编码与按照任务顺序编码的差距在何处
我们先定义一些概念吧,为了看起来更加高大上一点。基于位置编码和基于顺序编码的方法是我们最常见的古老编码方法,我们称之为硬编码(Hard coding), 因为基于位置编码的话位置信息是确定的而基于顺序编码的话至少分配顺序是确定的。本文的优先权编码我们称之软编码(Soft coding),因为其位置和顺序的信息都不是完全确定的。
其实优先权编码和按照顺序的编码是有很大的相似性的。首先前面我已经介绍过了,优先权的编码在满足先序约束的时候能够提高它的高效性。按照顺序的编码(简称:顺序编码)也是满足先序约束的。只是在分配的时候优先权编码考虑到了局部的序列空闲时间和结尾处负荷动平衡对于一些任务的权重有所提升,所以有局部的自适应性。顺序编码,相反地,相当于一个完全固定的套路,这就是软编码的一个好处。
但是在某种程度上两者又是基本等价的:如果给顺序编码加入一个局部搜索,那么基本就是一回事了,这个搜索不能再结束后再来局部搜索,因为现在的分配对于后续的位置影响是至关重要的。(顺便一提:我们基于位置的编码平时都是考虑序列空闲时间的) 所以其实优先权编码只是把以往的顺序编码换了一个含义,但是这就是一个很大的进步。但是,我们要说,顺序编码无法实现优先权编码的一个能力:特殊的约束。(还是顺便一提:基于位置解码我目前是可以考虑约束的,基本方法一致) 正是这个原因的存在所以基于优先权编码可以在某种程度上大幅提高获得可行解的可能性,从而获得更佳的解。
P2:本文的搜索策略如何解读
首先我们着眼于简单的分析,考虑一个再平衡解(初始的编码就相当于一个初始解)。我们改变的任务都是基于单个任务改变的组合。这就是本文说的局部搜索,这个方法张亚辉之前的论文已经发表,在拉动式和推动式的算法总提到,每次只改变一个任务。同时为了避免陷入局部最优,在达到局部最优时候加入一定概率接受稍差解,然后继续搜索。本文也是通过一定的优先级选择任务一一变动,直到达到局部最优(所有的改变都不能更加优秀)。区别就在于跳出局部最优的方法上。本文采用的方法是每次改变多个任务,就是本文的搜索主循环。这的确是一个很好的方法,相当于模拟了遗传算法的变异。使得搜索的广度(任务大分布,通过同时调整多个任务改变),和搜索深度(局部搜索)很好的结合。虽然在解码上本文也有点区别,但是在没有约束的时候这不应该是主要的差距;在包含约束的时候应该采用本文的解码或者基于位置的解码更加高效。
换个角度我们再来审视这个问题。转配线任务规划的一个难点在于后续的好坏与前面所有的分配关系都很大,所谓牵一发动全身。所以我们所用的树分支算法反向扩展枝叶的方法前馈比较差,前向搜索的速度慢(后面的分支实在太多了),所以效果自然也要打折扣,我也想象了很多的方法来解决这个问题,这不是根本的解决办法。而遗传算法和本文的算法(同时改变多个来任务的顺序,在时间分布上是随机的)都能达到这样一个更佳的效果,意味着全局前后的调整是比较随机的、均衡的。最近吴传珣同志(就是本人)正在研究蒙特卡洛树结构是一种新型的结构,也是为了解决这个问题,基于本文我觉得可以结合搜索树和优先权编码。
Others
比如最佳节拍的获得,通过逐步减一操作获得最佳节拍也是没有办法的事情啊,可以借鉴我指出的二分法加以变化。这个参数的设计和结果中每个成分的贡献比例需要向本文学习,清晰的对比可以看出各部分的贡献。本文还有一个重要的贡献在于,解码的过程中约束的处理上利用的数值分析,获得了一个更加简洁的方式,虽然和使用判断的方法可以达到一致的效果,但是使用数学的矩阵使得表述更加清晰,编程也更加方便。由于本文采用的方法具有随机性,所以作者也提到了我们不仅要关心结果的最优解,也要考虑分布尽量集中。统计的数据在本文得到了充分的利用,具有很强的说服力。最后提及一下本文采用的cost function 或者说是目标函数(适应度函数),虽然前人的经验在此,但是这个目标函数还是很不错的,考虑到了序列空闲时间和结尾空闲时间的权重,同时也考虑到了两部分在不同位置间的平衡度。 显然可以看出如果系数$w_1 \; and\; w_2$ 一样,那么前面两部分就是所有的空闲时间,换句话说就是最大化负荷。
Acknowledgment
本文的编码很有创新(减少了搜索的空间,因为每一次解码相当于这个空间乘以一定的倍数),虽然同时改变多个任务同样适用于顺序编码,但是这个创新点不能被埋没,因为它将遗传算法的核心移植到了本算法。随便一提,我需要指出其中的一点不足,因为我们改变的任务都被移送到了末尾(这里移动任务不保序,我觉得可以加入修正),相当于改变的任务都是靠后分配的(正是这个原因导致改变的任务不要太多,不然效果反而不如改变更少),这是一个缺点,但是目前也没有可替代的方案可以同时规划多个任务,所以保留观点(这个原理等同于序列最小化原理,将多变量问题看成单变量问题集合)。幸运的是本文还引入了局部搜索,弥补了上面的不足,所以整体效果不错。You Do An Excellent Job!