Quantization error is the difference between the analog signal and the closest available digital value at each sampling instant from A/D converter. Quantization error also introduces noise,to the sample signal.

Relations

The higher the resolution of A/D converter, the lower the quantization error and the smaller the quantization noise. The relationship between resolution (in bits) and quantization noise for ideal A/D converter can be expressed as Signal to Noise (S/N)=-20*log(1/2^n) where n is the resolution of A/D converter in bits. S/N is the signal to noise expressed in dB. This relationship can also be approximated as S/N=6n. Typical S/N ratios for ideal A/D converters are 96dB for 16 bits,72bB for 12 bits,and 48dB for 8 bits.

Quantization

The following figure shows how an analog signal gets quantized. The blue line represents analog signal while the brown one represents the quantized signal.

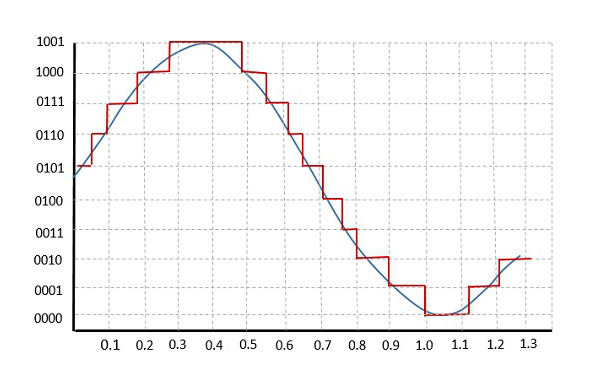
Both sampling and quantization result in the loss of information. The quantity of a Quantizer output depends upon the number of quantization levels used. The discrete amplitudes of quantized output are called as representation levels or reconstruction levels. The spacing between the two adjacent(相邻的) representation levels is called a quantum or step-size.

Types of Quantization

There are two types of quantization:

The type of quantization in which the quantization levels are uniformly spaced is termed as a uniform quantization. The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as Non-uniform quantization.

There are two types of uniform quantization:

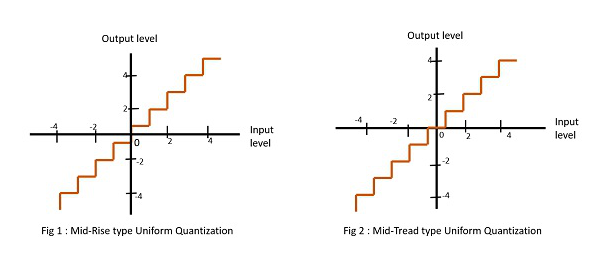
Figure 1 shows the mid-rise type and figure 2 shows the mid-tread type of uniform quantization.

• The Mid-Rise type is so called because the origin lies in the middle of a raising part of the stair-case like graph. The quantization levels in this type are even in number.

• The Mid-tread type is so called because the origin lies in the middle of a tread of the stair-case like graph. The quantization levels in this type are odd in number.
• Both the mid-rise and mid-tread type of uniform quantizer are symmetric about the origin.

Compute Quantization Error

This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods.

q = quantizer([8 7]);			%8表示8位表示精度，其中7位为小数点后表示精度，小数精度为1/2^7
r = realmax(q);
u = r*(2*rand(50000,1) - 1);    % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);  %取了两个误差长度的区间

%Fix: Round Towards Zero. Ther are floor,ceil,nearest,convergent for choise
q = quantizer('fix',[8 7]);
err = quantize(q,u) - u; 		%量化并求取误差
f_t = errpdf(q,xi); 			%the probability density function f
mu_t = errmean(q); 				%误差均值
v_t  = errvar(q);

fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err) %plot errpdf and err relation